Permutations and combinations are fundamental Mathematics concepts, especially for students pursuing SAT and A Levels. In this guide, we will delve into the basics of permutations and combinations and equip you with the knowledge to tackle SAT and A Level Maths questions.
What are Permutations and Combinations?
What are Permutations?
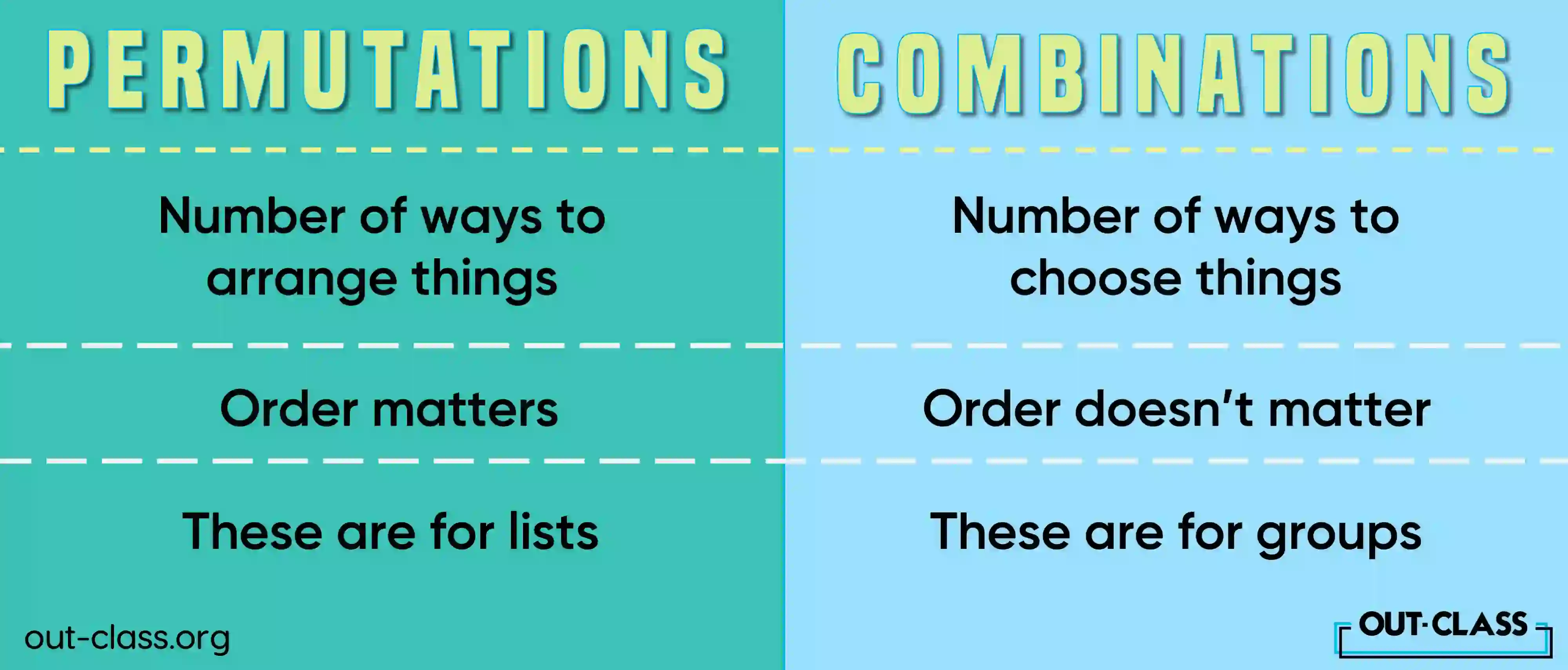
Permutations involve the arrangement of objects in a specific order. Imagine you have a set of distinct items and you want to know how many different ways you can arrange them.
How to calculate permutations:
The formula for permutations is given by:
P(n,r) = n!/(n-r)!
n represents the total number of items
r is the number of items to be arranged
What are Combinations?
Combinations, on the other hand, focus on selecting items without considering their order. Suppose you have a group of objects and you want to determine how many ways you can choose a subset of them.
How to calculate combinations:
The formula for combinations is:
C(n,r) = n!/(n−r)!r!
n is the total number of items
r is the number of items to be chosen
Difference Between Permutations and Combinations
It's crucial to grasp the distinction between permutations and combinations. Permutations highlight the order of arrangement, while combinations only consider the selection of items without any specific order. This understanding is paramount when approaching SAT and A Level Math questions that involve both concepts.
Why are Permutations and Combinations Important?
Now that we've laid the foundation, let's explore a few scenarios where permutations and combinations come into play.
Permutations and Combinations in A Level and SAT Questions:
A Level and SAT Math often present questions that challenge students to apply permutations and combinations. These questions may involve arranging students in a line, selecting a committee from a group, or forming teams for a competition. Let's look at a few permutations and combinations A Level and SAT question examples to illustrate these concepts:
-
Arranging Students in a Line:
Question: “In how many ways can five students be arranged in a line for a photograph?”
Solution: Using P(5,5) = 5!/(5-5)! = 5! = 120 ways -
Selecting a Committee:
Question: “If there are eight students, how many different committees of three can be formed?”
Solution: Employing the combination formula, C(8,3) = 8!/(8−3)!3! = 56 committees
Permutations and Combinations Practice
To solidify your understanding, consistent practice is key. Seek out permutations and combinations of questions in textbooks, online resources, and practice exams. Work through various scenarios to develop the skills needed to tackle any permutation or combination problem that may arise in your A Level Math and SAT examination.
Conclusion
In conclusion, mastering permutations and combinations A Level Math is integral to success. Armed with a solid understanding of the concepts, the difference between permutations and combinations, and a knack for applying permutations and combinations formulas, you'll be well-prepared for any SAT or A Level Math question that comes your way. Remember to practice regularly, and soon you'll approach permutations and combinations of SAT and A Level Math with confidence and ease.
FAQs
Q. What are permutations?
Permutations involve the arrangement of objects in a specific order. The number of permutations of a set of items is calculated using the formula P(n,r) = n! / (n-r)!, where n is the total number of items and r is the number of items to be arranged.
Q. What are combinations?
Combinations focus on selecting items without considering their order. The number of combinations is calculated using the formula C(n,r) = n! / [(n-r)! r!], where n is the total number of items and r is the number of items to be chosen.
Q. What is the difference between permutations and combinations?
The key difference is that permutations consider the order of the items, while combinations do not. Permutations are used for arrangements, whereas combinations are used for selections.
Q. How can I calculate the number of permutations of 5 students arranged in a line?
The number of permutations of 5 students arranged in a line is calculated using the formula P(5,5) = 5! / (5-5)! = 5! = 120 ways.
Q. How can I calculate the number of ways to form a committee of 3 from 8 students?
The number of combinations to form a committee of 3 from 8 students is calculated using the formula C(8,3) = 8! / [(8-3)! 3!] = 56 ways.
Q. What is the formula for permutations?
The formula for permutations is P(n,r) = n! / (n-r)!, where n is the total number of items and r is the number of items to be arranged.
Q. What is the formula for combinations?
The formula for combinations is C(n,r) = n! / [(n-r)! r!], where n is the total number of items and r is the number of items to be chosen.
Q: How do permutations and combinations questions appear in A Level and SAT exams?
Questions may involve scenarios such as arranging students in a line, selecting a committee from a group, or forming teams for a competition, requiring you to apply the appropriate formulas and concepts.