In Mathematics, every value has a role to play. Even zero! Why, you ask? Because zero is considered the root of all polynomials, i.e. the solutions of common arithmetic expressions (except polynomials can contain more than two terms).
In this article, we are going to break down the definition of polynomial equations and what it means to find the zero of a polynomial.
What is a Polynomial?
A polynomial is an algebraic expression that consists of variables, coefficients and exponents. An example can be found below:
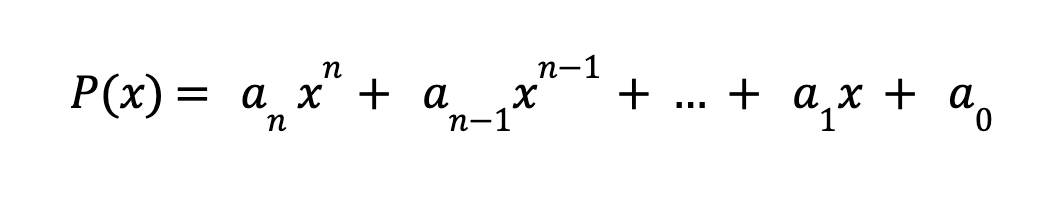
Where:
-
P(x) is the polynomial
-
an , an-1 , … , a1 , a0 are coefficients
-
x is the variable
What is the Zero of a Polynomial?
The zero of a polynomial is the value of the variable x for which the polynomial equates to zero. In other words, if P(c) = 0, then c is the zero of the polynomial P(c).
Now, when we say the zero of a polynomial, what we are referring to is the value of x that makes the polynomial equal to zero. Such values have significance when it comes to graphing polynomials and solving them. Other reasons for finding the zero of a polynomial include:
-
Roots or Solutions: When you set the polynomial equal to zero and solve for the variable, you find the values for which the polynomial equates to zero. These values are the solutions to the polynomial equation.
-
Graphical Interpretation: The zeros of a polynomial are the points where the polynomial intersects the x-axis on a graph. These ultimately help in sketching the graph of a polynomial.
-
Factorization: Knowing the zeros of a polynomial allows you to factorise it. For example, consider the polynomial P(x) = x2 – 4. To find its zeros, we must set P(x) to be equal to zero and then solve for x:
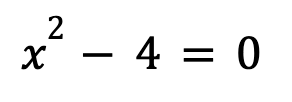
After factoring the polynomial, the equation changes to the following: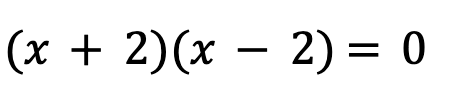
Now, by setting each factor to be equal to zero and then solving for x, we come up with the following: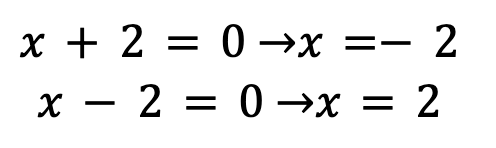
So, the zeros of the polynomial P(x) = x2 – 4 are x = -2 and x = 2.
-
Solving Equations: Polynomial equations are often solved by finding their zeros. If you have a polynomial equation that is set to zero, finding the zeros then provides the solution to the equation.
-
Understanding Behavior: The zeros of a polynomial provide information about its behavior. They help determine the points where the polynomial changes from positive to negative and vice versa along with the intervals where they undergo these changes.
Does the Polynomial Have to Equate to Zero?
When we talk about the zeros of a polynomial, we are referring to the values of the variable (often denoted as x) for which the polynomial evaluates to zero. While the polynomial itself does not need to always equate to zero, finding its zeros involves setting it equal to zero to determine the value of the variables that make it zero.
Related: Permutations and Combinations Explained
How to Find the Zero of a Polynomial – An Example
For ease of understanding, let us take the case of a polynomial representing the cost of manufacturing a product as a function of the number of units produced.
The cost function C(x) will be given as follows:
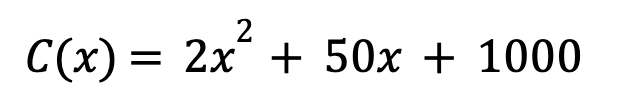
Where:
-
x is the number of units produced
-
C(x) is the total cost of producing x units
To find the number of units that help minimize cost, we need to first find the derivative of the function. The minimum will appear when the derivative is equal to zero.
A derivative represents the rate at which a function is changing at any given point. In other words, it is defined as the limit of the average rate of change of the function as the interval over which the change is calculated becomes small.
In our example, we will need to find the derivative C1(x) by applying the power rule which states that if 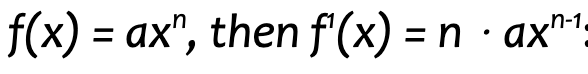
Derivative for the term 2x^2:
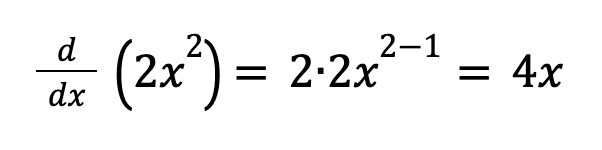
Derivative for the term 50x:
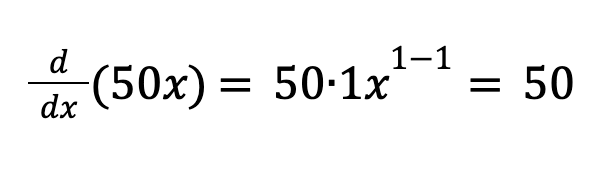
Derivative for the constant term 1000:
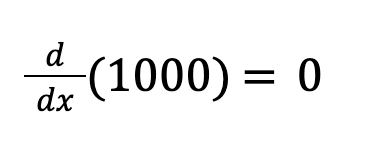
(The derivative of a constant is always zero).
Combine the derivatives of each term:
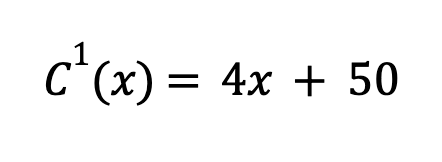
Now, we set the derivatives to be equal to zero and solve for x:
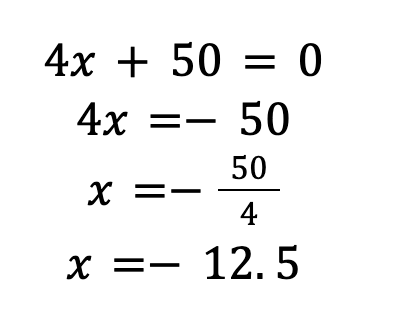
So, the critical point, i.e. when the derivative is equal to zero, is equal to -12.5. However, when we think of this in the context of the number of units produced, it doesn’t make much sense to include a negative number. Hence, we will discard the negative value.
Now that we have the value for x, we can input that value into our cost function to find the minimum cost
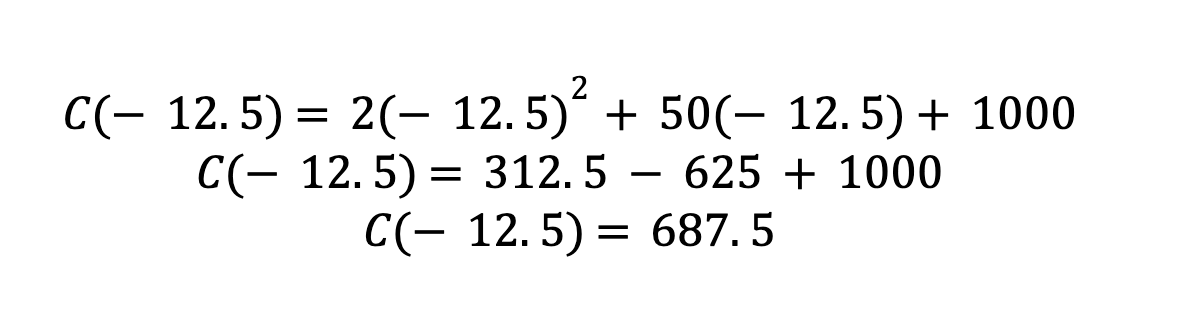
This shows that the number of units needed to produce the minimum cost of 687.5 is 12.5. As mentioned above, since the number of units cannot be a negative figure, for the sake of understanding, we will discard the negative value.
Conclusion
By making the polynomial equal to zero and solving for the variable, you will be able to find the values for which the polynomial equates to zero. These values are the solutions to the polynomial equation. If you want to find out more about polynomials, head on to www.out-class.org


